Numerical Modeling of Earthquake Cycles Based On Navier-Stokes Equations With Viscoelastic-Plasticity Rheology

Numerical models assume different governing equations and constitutive relations depending on the dominant time- and length-scales for the problem. The timescales associated with changes in whole mantle flow are typically of the order of tens to hundreds of thousands of years and, as a result, it is usual to neglect the unimportant inertial terms and it is often unnecessary to consider the effects of elastic stresses. Such models are usually formulated on the assumption of creeping viscous flow following the Stokes equations. The dynamics of deformation within the lithosphere is dominated by localizing phenomena (shear banding and faulting) that are commonly modeled with visco-elastic-plastic rheology. These models require significantly higher spatial and temporal resolution compared to whole-mantle flow models to capture the stress-redistribution that is associated with the creation, propagation of localized structures and the offsets that occur along their length. Plastic models of localization assume a static equilibrium with any time-dependence resulting from the evolution of damage variables or geometry (e.g., interfaces, surface topography). By contrast, at the shorter timescales associated with the individual ruptures of a fault, the largest terms in the equation of motion come from accelerations and the elastic response of the medium.

In this paper, we discuss our approach to include inertial terms into the open-source Underworld geodynamics modeling framework. This code was originally designed to address coupled problems in mantle-lithosphere dynamics using a history-dependent, viscoelastic-plastic formulation of the Stokes equations with a particle-in-cell approach to track elastic stresses during fluid deformation. Fluid acceleration can also be tracked using the Lagrangian particle swarm, which we demonstrate through a series of standard benchmarks of the Navier-Stokes problem (Fig. 1ab).

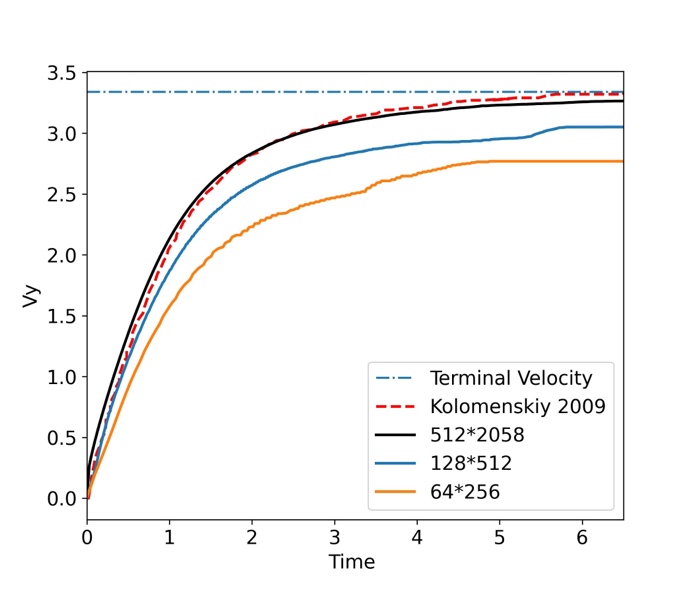
Figure 1. The left panel shows a falling cylinder in fluid. The right panel demonstrates the velocity of the falling cylinder starting from rest to steady state. The horizontal line at Vy = 3.34 marks the terminal velocity. The red dashed line is the result from Kolomenskiy and Schneider (2009). Solid lines with different mesh resolutions are from Underworld.

A second benchmark is to compare the speed of a shear-wave through a viscoelastic medium for which analytic solutions are available (Fig. 2).

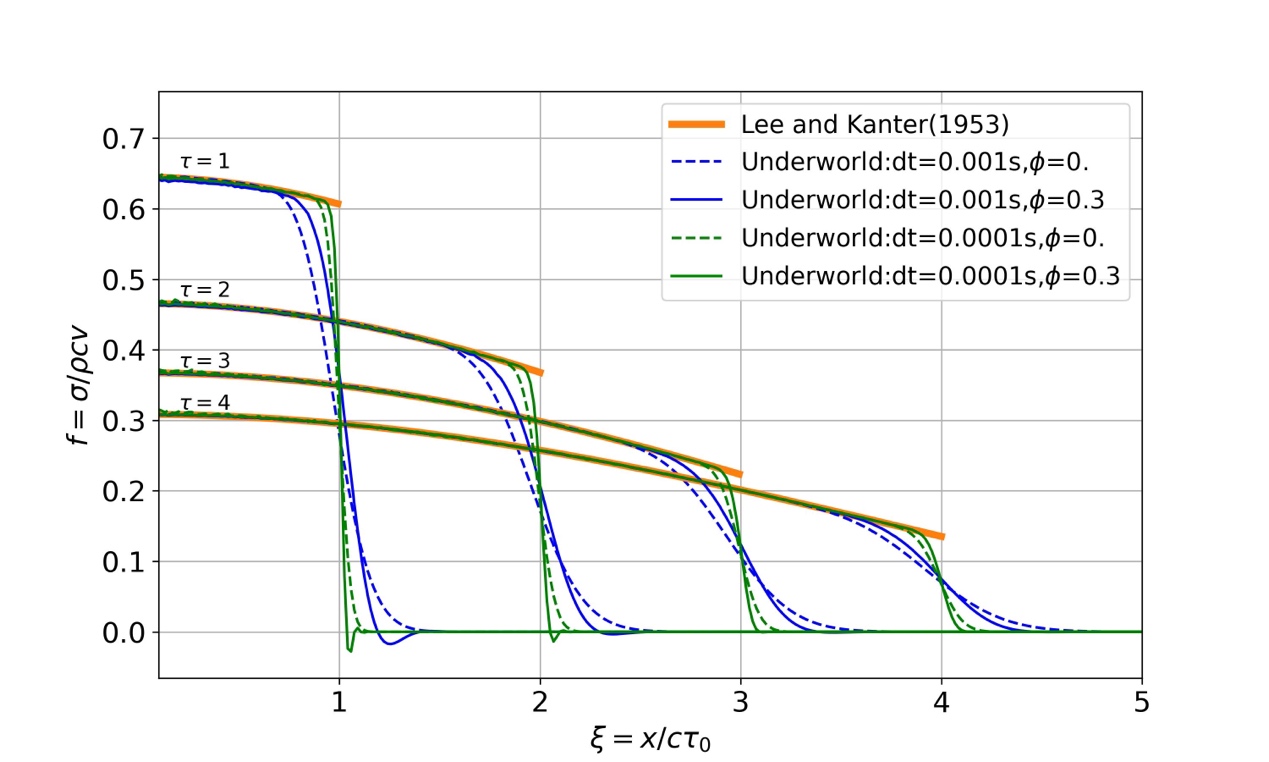
Figure 2. Wave propagation along a Maxwell rod. The dimensionless stress f is plotted against dimensionless distance ξ for the dimensionless time τ between 0 and 8. The solid orange thick orange line is an analytical solution from Lee and Kanter (1953) while other blue and green lines are produced by Underworld for different temporal resolutions (dt) and truncation precisions (φ). The dimensionless stress is described by the Heaviside step function. And when the wave front reaches ξ = 1 at τ = 1, and the stress is zero ahead of this front (ξ > 1).

In addition, we compare this code with the community code verification exercise for 3D dynamic modeling of sequences of earthquakes and aseismic slip (Fig.3).

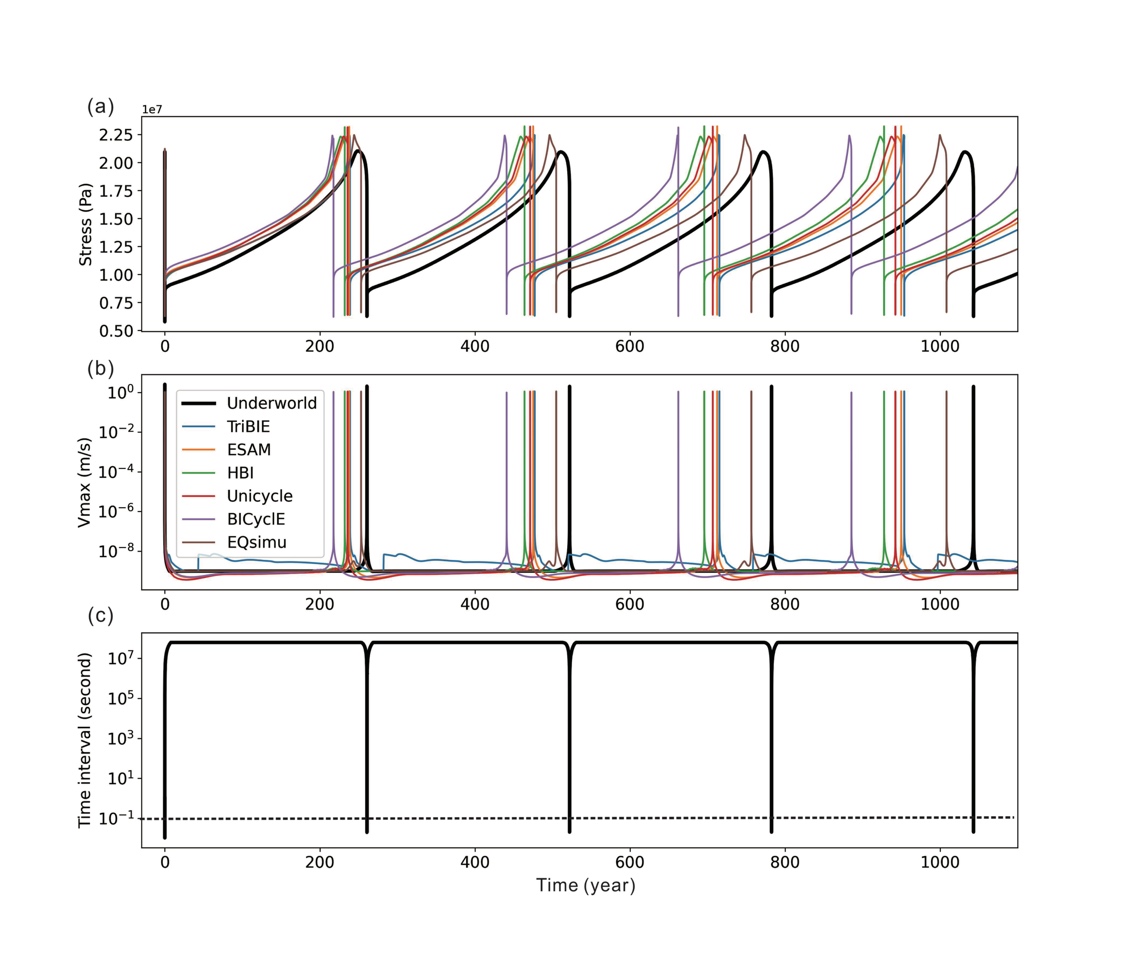
Figure 3. Evolution of the stress at the reference point (0, 0, −10 km) (a), maximum slip rate along the entire fault zone (b) and the adaptive time step used in simulation (c) for the reference model.

We finally apply our new 3D code for generic models of inter-seismic deformation of thrust faults and discuss how we can use surface geodetic observations to infer the strength of the lower crust and activity of faults in stable cratons (Fig. 4).

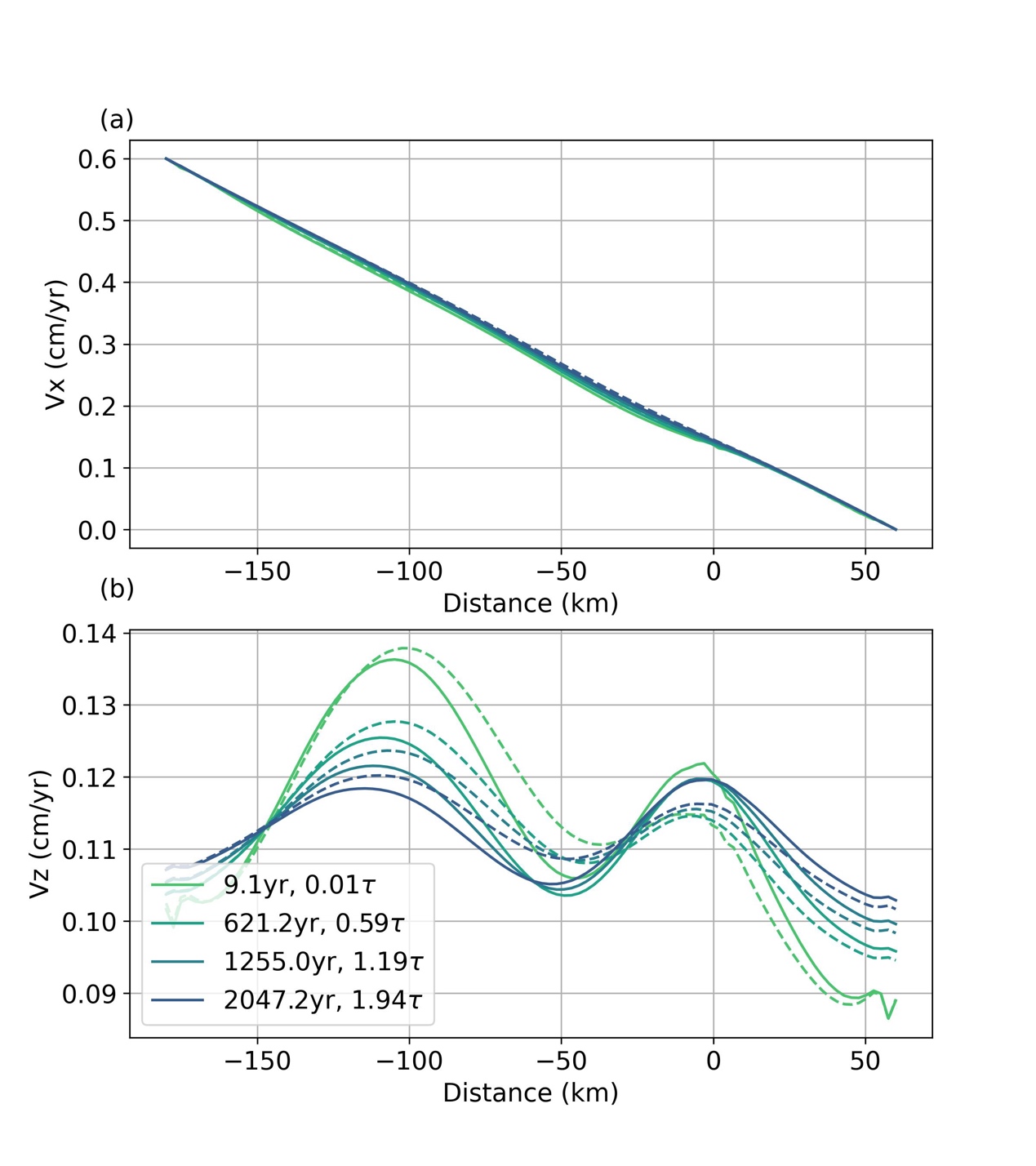
Figure 4. Horizontal (Vx) and vertical (Vz) post/inter-seismic movement at the top surface of the three-dimensional model for the profile at y = 0 km (solid line) and y = −22.5 km (dashed line). The legend represents the absolute time (left column) and the time relative to the characteristic relaxation time τ (right column).

Haibin Yang, the first author and the corresponding author of this paper, is now an assistant Professor at School of Earth Sciences, Zhejiang University. This research was funded by the National Natural Science Foundation of China (Grant No. 42030306). Testing models are run with gadi in the National Computational Infrastructure (Canberra) and setonix in Pawsey (Perth).

Article information: Yang, H., Moresi, L., Weng, H., & Giordani, J. 2023. Numerical modeling of earthquake cycles based on Navier-Stokes equations with viscoelastic-plasticity rheology. Geochemistry, Geophysics, Geosystems, 24, e2023GC010872. https://doi. org/10.1029/2023GC010872